近日,开云(中国)海气相互作用研究团队利用全球热带锚系浮标观测揭示了风场日内变化在海气动量通量中的关键作用。该研究成果“Key role of subdaily wind variability for tropical surface wind stress”发表在Journal of Physical Oceanography,闫运伟教授为论文第一作者兼通讯作者,合作者包括学院宋翔洲教授和英国国家海洋学中心Marilena Oltmanns博士。
海气动量通量(海表风应力)是全球大洋环流的主要驱动力,调控着海洋的质量、动量和能量再分布。此外,风应力可改变海洋混合,进而影响海水温盐特性。由于风应力与风场之间的关系是非线性的,风场高频变化能够调制低频的风应力。已有大量研究表明天气尺度风场对平均风应力有显著贡献。同样,风场日内变化也可以影响平均风应力,进而改变上层海洋温盐结构。但目前已有的工作主要集中在个别观测点或航次,在全球尺度上,风场日内变化对平均风应力的贡献如何还不清楚。
研究团队利用全球热带锚系浮标量化了海表风场日内变化对平均风应力的贡献(如图1所示):在热带海域,海表风场日内变化对平均风应力的贡献为6.5×10-3 N/m2(12.4%);空间上,风场日内变化的贡献在ITCZ区较大,最大贡献百分比位于赤道西太平洋,其值为28.5%。进一步分析表明风场日内变化的贡献大小主要由其动能决定。目前常用的再分析数据ERA5和MERRA2显著低估了风场日内变化对平均风应力的贡献,其误差百分比分别为51%和63%。由于动能的低估,ERA5和MERRA2中风场日内变化的贡献也被低估。假设使用这两个再分析数据的风场驱动海洋模式,低估的风场日内变化会导致输入热带海洋的总动量(风应力)减少7%和8%(如图2所示),降低数值模拟的准确度。为克服再分析数据的这一缺陷,团队发展了两套参数化方案来反映海表风场日内变化的贡献:一套与时间无关,另一套与时间有关,两套参数化方案都能再现风场日内变化贡献的~80%(如图3所示)。结合该参数化方案和天平均风场强迫海洋模式有潜力得到更为准确的模拟结果。
本研究得到了国家自然科学基金优秀青年科学基金项目和面上项目(41976028、42122040、42076016)资助。
相关论文信息:
Yan Yunwei*, Song Xiangzhou, & Oltmanns Marilena (2023). Key role of subdaily wind variability for tropical surface wind stress. Journal of Physical Oceanography, https://doi.org/10.1175/JPO-D-22-0156.1
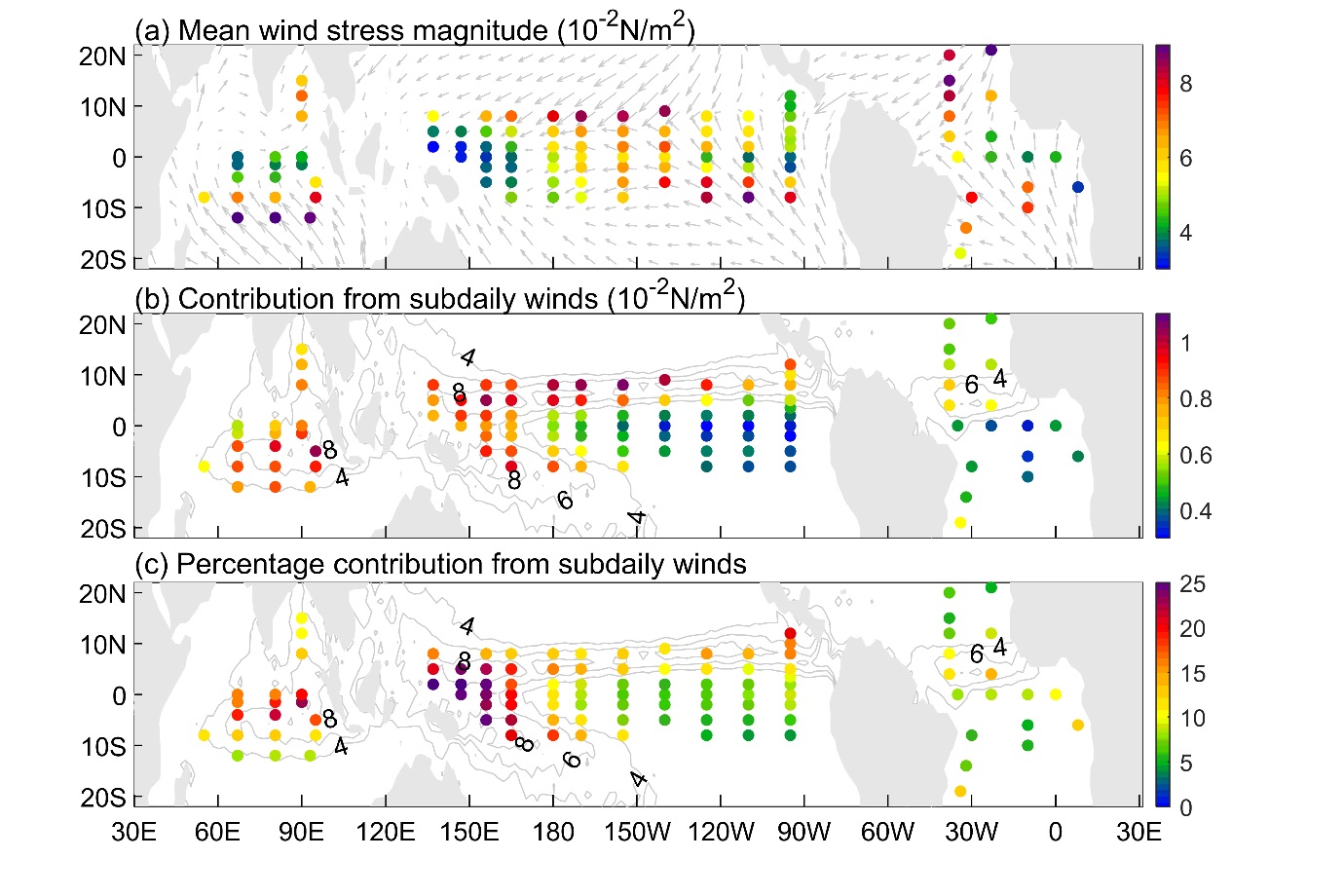
图1、(a)海表平均风应力。(b,c)风场日内变化对平均风应力的贡献及对应百分比。
Fig. 1. (a) Mean surface wind stress magnitude estimated from GTMBA observations. (b, c) Contribution from subdaily winds to the mean wind stress magnitude and the corresponding percentage. Gray arrows and contours denote the satellite-derived mean surface wind stress (a) and precipitation rate (mm/day, b, c), respectively. The satellite-derived mean wind stress was calculated from the Scatterometer Climatology of Ocean Winds (SCOW, Risien and Chelton, 2008).
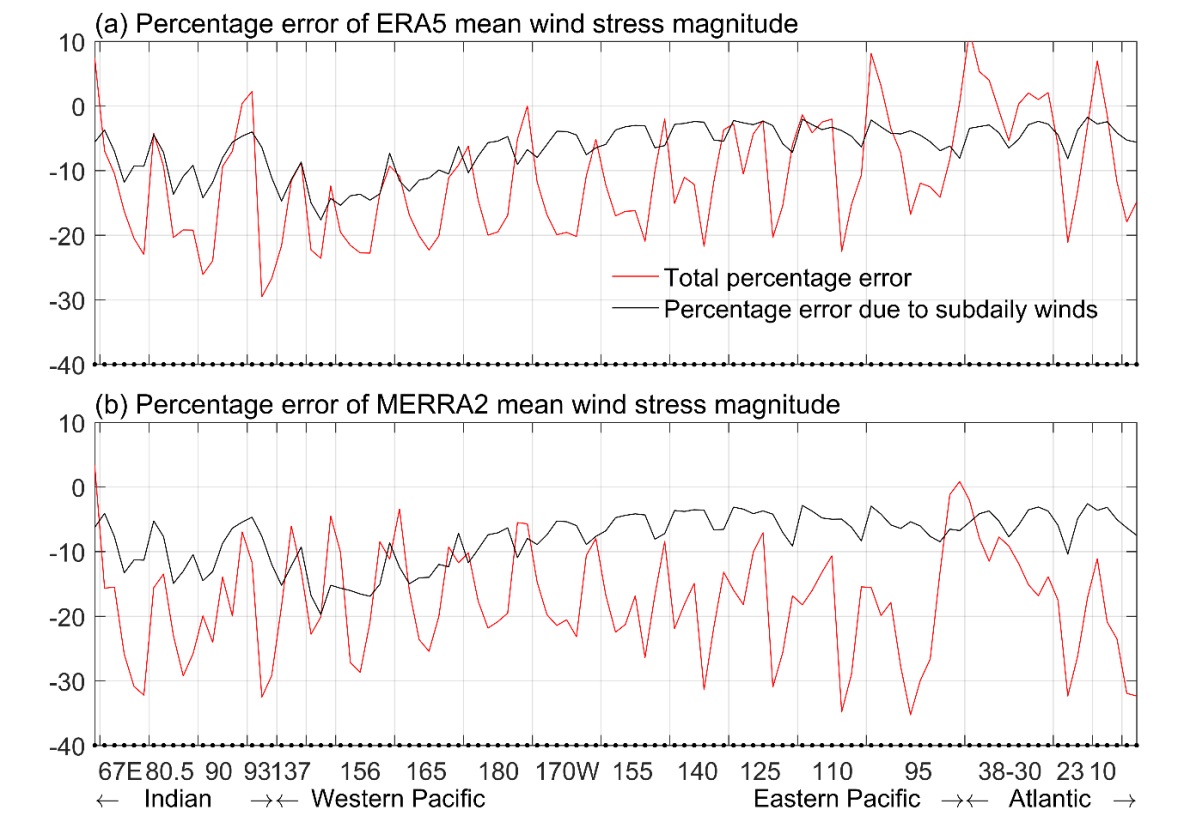
图2、再分析数据中平均风应力的误差百分比(红线)及由风场日内变化引起的误差百分比(黑线):ERA5(上图)、MERRA2(下图)。
Fig. 2. Percentage error (red curve) of the mean wind stress magnitude in the ERA5 (a) and MERRA2 (b) products based on the GTMBA observations. The black curve denotes the percentage relative error associated with inaccurate subdaily winds.
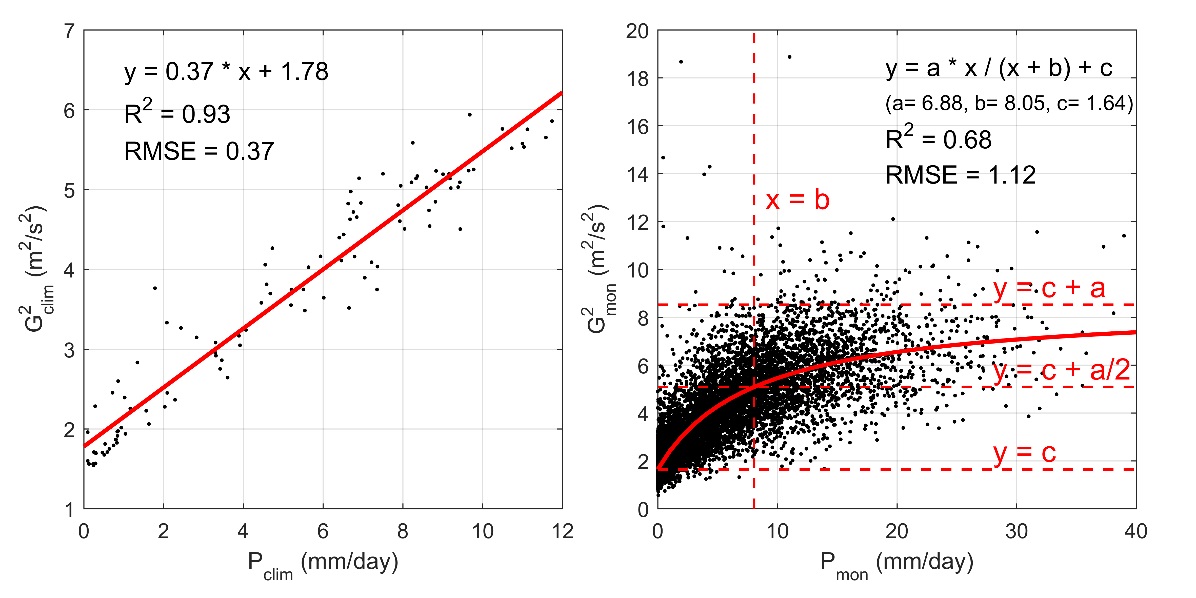
图3、阵风值与降水回归模型:与时间无关的模型(左图)和与时间相关的模型(右图)。
Fig. 3. Regression model between the square of the gustiness value (G^2) and precipitation rate (P) for the time-independent (left panel) and time-dependent (right panel) schemes.



